An article explaining non-Euclidean geometry recited the early endeavor of Gerolamo Saccheri to prove Euclid’s fifth postulate from the other postulates, to see if it was really necessary to have a fifth postulate. Efforts to prove the fifth postulate led to the method of assuming a proposition contrary to the fifth postulate, along with the other postulates, to see if a contradiction would arise.
From this arose the logical argument that begins with the idea that there must be some number of axioms leading up to one like the fifth postulate. So the idea follows that either such an axiom is not necessary, in which case you can prove it from the other axioms (by showing that given a contrary axiom a contradiction will arise), or, the axiom is necessary, in which case a contrary axiom should not produce a logical contradiction. The failure to produce a contradiction led to the idea that a consistent system with a non-Euclidean axiom could be possible.
The article also mentioned János Bolyai and Nikolai Lobachevsky in addition to Saccheri as early pioneers in the development of non-Euclidean geometry. The developments by all three of these early pioneers, however, began with proofs about angles! This means that, using Hilbert’s system as a guide, if it were overlaid back in time, it would have been assumed that the theorems at least up through Hilbert’s Theorem 12 (SAS) would not require a Euclidean fifth postulate equivalent for proof, or, in the case of Saccheri, that Hilbert’s Axiom I. 2 would not be present, otherwise a contradiction would occur. The assumption was an error.
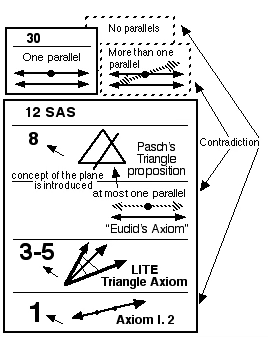
Hilbert is the one who put the axiomatic foundation of geometry on a rigorous basis with the coordinate line included, but it turned out that in the early stages of Hilbert’s system, axioms contrary to the non-Euclidean systems had actually been present, tacitly. (The Note at the link below describes this.) So that logical argument posed for the development of the non-Euclidean geometries still holds, however, it was thought that 28 or so theorems could be proved without the need of an axiom contrary to a non-Euclidean system, and this turned out to be wrong. That need arises even earlier than Hilbert‘s Theorem 8, as seen in the diagram below.
An axiom used by Hilbert seen in the diagram above which he called “Euclid’s Axiom,” prescribed that through a point not on a line there is "no more than one parallel” to the line. (This axiom is the equivalent of the original Playfair's axiom which Playfair substituted for Euclid’s fifth postulate in 1795.)
Notice that by itself, the axiom would include the possibility of there being no parallels. Non-Euclidean geometry with no parallels is called Riemannian geometry. So “Euclid’s Axiom” is not by itself incompatible with the Riemannian geometry that says there are no parallels. However, when Axiom I. 2 is included with the other axioms of Hilbert, you can prove there is a parallel line, which contradicts the Riemannian geometry proposition that there are no parallels, as the diagram indicates. That Axiom I. 2 is incompatible with the Riemannian geometry is recognized and not disputed and cannot be reasonably disputed.
This is explained in the Note, a five minute read, at the link: Einstein's General Relativity is Based on Self-contradicting Non-Euclidean Geometry